क्षेत्रमिति - Mensuration
81. (i) Area of triangle = 1/2 × base × altitude
(ii) Area of triangle using heron’s formula= 
82. In an equilateral triangle with side a, then
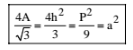 where A ® Area of triangle
where A ® Area of triangle
P ® Perimeter
h ® Height
83. In an isosceles triangle PQR


88. In a circle with radius r
A/C=D/4 Where A - Area of cricle
C - Circumference of circle
D - Diameter of circle
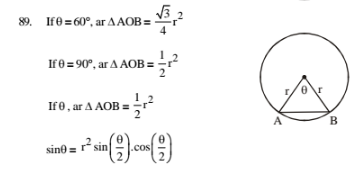
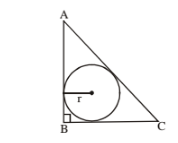
90. (i) A circle with largest area inscribed in a right angle triangle, then r =
(ii) If ABC is an equilateral triangle with side a, then Area of circle =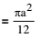
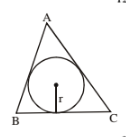
(iii) If ABC is an equilateral triangle with side a, then area of circle =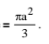
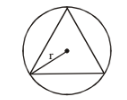
(iv) If DABC is an equilateral triangle, and two circles with radius r and R, then= 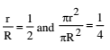
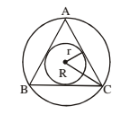
(v) Three equal circle with radius r and an equilateral triangle ABC, then area of shaded region =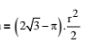
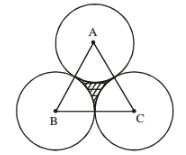
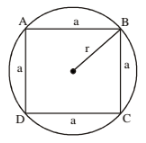
91. ABCD is a square placed inside a circle with side a and radius of circle r, then 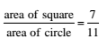
92. Diagonal of a cube= √3✖side
93. Diagonal of a cuboid 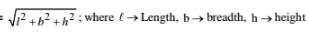
94. For two cubes 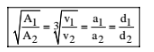
where A1, A2 ⇒ Area of cubes
v1, v2 ⇒ Volume
a1, a2 ⇒ Sides
d1, d2 ⇒ Diagonals
95. Units of Measurement of Area and Volume
The inter-relationships between various units of measurement of length, area and volume are listed below for ready reference:
Length
1 Centimetre (cm) =10 milimetre (mm)
1 Decimetre (dm) =10 centimetre
1 Metre (m) =10 dm = 100 cm = 1000 mm
1 Decametre (dam) =10 m = 1000 cm
1 Hectometre (hm) =10 dam = 100 m
1 Kilometre (km) =1000 m = 100 dam = 10 hm
1 Myriametre =10 kilometre
Area
1 cm2= 1 cm × 1 cm =10 mm × 10 mm = 100 mm2
1 dm2 = 1 dm × 1 dm =10 cm × 10 cm = 100 cm2
1 m2 = 1 m × 1 m =10 dm × 10 dm = 100 dm2
1 dam2 or 1 are =1 dam × 1dam = 10 m × 10 m = 100 m2
1 hm2 = 1 hectare =1 hm × 1 hm = 100 m × 10000m2 = 100 dm2
1 km2 = 1 km × 1 km =10 hm × 10 hm = 100 hm2 or 100 hectare
Volume
1 cm3 = 1 ml =1 cm × 1 cm × 1 cm = 10 mm × 10 mm × 10 mm = 1000 mm3
1 litre = 1000 ml =1000 cm3
1 m3 = 1 m×1 m×1m =100 cm × 100 cm × 100 cm = 106 cm3
=1000 litre = 1 kilometre
1 dm3 = 1000 cm3, 1m3 =1000 dm3, 1 km3 = 109 m3
If a, b, c are the edges of a cuboid, then
96. The longest diagonal= 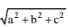
(i) If the height of a cuboid is zero it becomes a rectangle.
(ii) If “a” be the edge of a cube, then
(iii) The longest diagonal = a√3
97. Volume of pyramid = 1/3 ✖Base✖Area✖height (H)
98. (i) If A1& A2 denote the areas of two similar figures and l1 & l2 denote their corresponding linear measures, then= 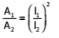
(ii) If V1 & V2 denote the volumes of two similar solids and l1 , l2 denote their corresponding linear measures, then= 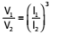
(iii) The rise or fall of liquid level in a container = Total volume of objects submerged or taken out Cross sectional area of container= 
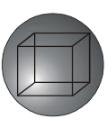
99. If a largest possible cube is inscribed in a sphere of radius ‘a’ cm, then
(i) the edge of the cube = 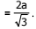
(ii) If a largest possible sphere is inscribed in a cylinder of radius ‘a’ cm and height ‘h’ cm, then for h > a,
a. the radius of the sphere = a and
b. the radius = h/2 (for a > h)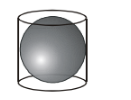
(iii) If a largest possible sphere is inscribed in a cone of radius ‘a’ cm and slant height equal to the diameter of the base, then
a. the radius of the sphere= a/√3. 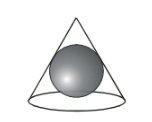
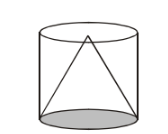
(iv) If a largest possible cone is inscribed in a cylinder of radius ‘a’ cm and height ‘h’ cm, then the radius of the cone = a and height = h.
(v) If a largest possible cube is inscribed in a hemisphere of radius ‘a’ cm, then the edge of the cube =a√2/3
100. In any quadrilateral
Area = 1/2✖one diagonal✖(sum of perpendiculars to it from opposite vertices) = 1/2 × d (d1 + d2)
(ii) Area of a cyclic quadrilateral= 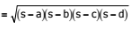 where a, b, c, d are sides of quadrilateral and
where a, b, c, d are sides of quadrilateral and
s = semi perimeter= 
101. If length, breadth & height of a three dimensional figure increase/decrease by x%, y% and z%, then
Change in area= 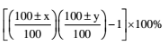
Change in Volume = 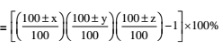
No comments:
Post a Comment