संख्या प्रणाली - Number System

संख्या प्रणाली - Number System

1. Method to multiply 2-digit number.

(i) AB × CD = AC / AD + BC / BD

35 × 47 = 12 / 21 + 20 / 35 = 12 / 41 / 35 = 1645

(ii)AB × AC = A² / A (B + C) / BC

74 × 76 = 7² / 7(4 + 6) / 4 × 6

= 49 / 70 / 24 = 4⁹ / 7⁰ / 2⁴ = 5624

(iii)  AB × CC = AC / (A + B)C / BC

= 35 × 44 = 3 × 4 / (3 + 5) × 4 / 5 × 4

= 12 / 32 / 20 = 1² / 3² / 2⁰ = 1540

2. Method to multiply 3-digit no.

ABC × DEF = AD / AE + BD / AF + BE + CD / BF + CE / CF

456 × 234 = 4 × 2 / 4 × 3 + 5 × 2 / 4 × 4 + 5 × 3 + 6 × 2 / 5 × 4 + 6 × 3 / 6 × 4

= 8 / 12 + 10 / 16 + 15 + 12 / 20 + 18 / 24

= 8 / 2² /4³ / 3⁸ / 2⁴ = 106704

3. If in a series all number contains repeating 7. To find their sum, we start from the left multiply 7 by 1, 2, 3, 4, 5 & 6. Look at the example bel

777777 + 77777 + 7777 + 777 + 77 + 7 = ?

= 7 × 1 / 7 × 2 / 7 × 3 / 7 × 4 / 7 × 5 / 7 × 6

= 7 / 1⁴ / 2¹ / 2⁸ / 3⁵ / 4² = 864192

4. 5555 + 0.555 + 0.55 + 0.5 = ?

To find the sum of those number in which one number is repeated after decimal, then first write the number in either increasing or decreasing order. Then -find the sum by using the below method.

0.5555 + 0.555 + 0.55 + 0.5

= 5 × 4 / 5 × 3 / 5 × 2 / 5 × 1

= 2⁰ / 1⁵ / 1⁰ / 5 = 2.1605

5 Those numbers whose all digits are 3.

(33)² = 1089        

Those number. in which all digits are number is 3 two or more than 2 times repeated, to find the square of these number, we repeat 1 and 8 by (n – 1) time. Where n ® Number of times 3 repeated.

(333)² = 110889

(3333)² = 11108889

6. Those number whose all digits are9.

(99)² = 9801

(999)² = 998001

(9999)2 = 99980001

(99999)² = 9999800001

7. Those number whose all digits are

A number whose one’s, ten’s, hundred’s digit is 1 i.e., 11, 111, 1111, ....

In this we count number of digits. We write 1, 2, 3, ..... in their square the digit in the number, then write in decreasing order up to 1.

11²     = 121

111²   = 12321

1111² = 1234321

8. Some properties of square and square root:

(i)    Complete square of a no. is possible if its last digit is 0, 1, 4, 5, 6 & 9. If last digit of a no. is 2, 3, 7, 8 then complete square root of this no. is not possible.

(ii)   If last digit of a no. is 1, then last digit of its complete square root is either 1 or 9.

(iii)  If last digit of a no. is 4, then last digit of its complete square root is either 2 or 8.

(iv)  If last digit of a no. is 5 or 0, then last digit of its complete square root is either 5 or 0. (v)   If last digit of a no. is 6, then last digit of its complete square root is either 4 or 6.

(vi)  If last digit of a no. is 9, then last digit of its complete square root is either 3 or 7.

9. Prime Number :

(i)    Find the approx square root of given no. Divide the given no. by the prime no. less than approx square root of no. If given no. is not divisible by any of these prime no. then the no. is prime otherwise not.

For example : To check 359 is a prime number or not.

Sol. Approx sq. root = 19

Prime no. < 19 are 2, 3, 5, 7, 11, 13, 17

359 is not divisible by any of these prime nos. So 359 is a prime no. For example: Is 2⁵⁰⁰¹ + 1 is prime or not? 

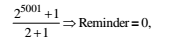
 2⁵⁰⁰¹ + 1 is not prime.

(ii)   There are 15 prime no. from 1 to 50.

(iii)   There are 25 prime no. from 1 to 100.

(iv)  There are 168 prime no. from 1 to 1000.

10. If a no. is in the form of xⁿ + aⁿ, then it is divisible by (x + a); if n is odd.

11. If xⁿ (x – 1), then remainder is always

12. If xn(x + 1)

(i)    If n is even, then remainder is 1.

(ii)   If n is odd, then remainder is x.

14. Number of divisors : 

(i)    If N is any no. and N = aⁿ × b^m × c^p × .... where a, b, c are prime no.

No. of divisors of N = (n + 1) (m + 1) (p + 1) ....

e.g. Find the no. of divisors of 90000.

N = 90000 = 2² × 3² × 5² × 10² = 2² × 3² × 5² × (2 × 5)² = 2⁴ × 3² × 5⁴

So, the no. of divisors = (4 + 1) (2 + 1) (4 + 1) = 75

(ii)   N = aⁿ × b^m × c^p, where a, b, c are prime

Then set of co-prime factors of N = [(n + 1) (m + 1) (p + 1) – 1 + nm + mp + pn + 3mnp]

To find the last digit or digit at the unit’s place of aⁿ.

If the last digit or digit at the unit’s place of a is 1, 5 or 6, whatever be the value of n, it will have the same digit at unit’s place, i.e.,

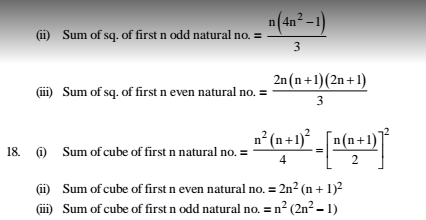
(i) xⁿ – yⁿ is divisible by (x + y) When n is even

       (ii) xⁿ – yⁿ is divisible by (x – y) When n is either odd or even.

   20.  For any integer n, n³ – n is divisible by 3, n⁵ – n is divisible by 5, n¹¹ – n is divisible by 11, n¹³ – n is divisible by 13.

 

Some articles related to Divisibility :

 A no. of 3-digits which is formed by repeating a digit 3-times, then this no. is divisible by 3 and 37. e.g., 111, 222, 333, .......

A no. of 6-digit which is formed by repeating a digit 6-times then this no. is divisible by 3, 7, 11, 13 and 37. g., 111111, 222222, 333333, 444444, .............

 

22. Divisible by 7 : We use osculator (– 2) for divisibility test.

99995 : 9999 – 2 × 5 = 9989

9989 : 998 – 2 × 9 = 980

980 : 98 – 2 × 0 = 98

 Now 98 is divisible by 7, so 99995 is also divisible by 7.

 23. Divisible by 11 : In a number, if difference of sum of digit at even places and sum of digit at odd places is either 0 or multiple of 11, then no. is divisible by 11.

For example, 12342 ¸ 11

Sum of even place digit = 2 + 4 = 6

Sum of odd place digit = 1 + 3 + 2 = 6

Difference = 6 – 6 = 0

12342 is divisible by 11.

24.Divisible by 13 : We use (+ 4) as osculator

e. g., 876538 ¸ 13

876538: 8 × 4 + 3 = 35

5 × 4 + 3 + 5 = 28

8 × 4 + 2 + 6 = 40

0 × 4 + 4 + 7 = 11

1 × 4 + 1 + 8 = 13

13 is divisible by 13.

 876538 is also divisible by 13.

25. Divisible by 17 : We use (– 5) as osculator.

e. g., 294678: 29467 – 5 × 8 = 29427

27427: 2942 – 5 × 7 = 2907

2907: 290 – 5 × 7 = 255

255: 25 – 5 × 5 = 0

 294678 is completely divisible by 17.

26. Divisible by 19 : We use (+ 2) as osculator.

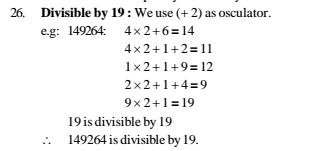
27. HCF (Highest Common factor)

There are two methods to find the HCF–

(a)   Factor method           (b)  Division method

 1. For two no. a and b if a < b, then HCF of a and b is always less than or equal to a .

 2. The greatest number by which x, y and z completely divisible is the HCF of x, y and z.

3. The greatest number by which x, y, z divisible and gives the remainder a, b and c is the HCF of (x –a), (y–b) and (z–c).

4. The greatest number by which x, y and z divisible and gives same remainder in each case, that number is HCF of (x–y), (y–z) and (z–x).

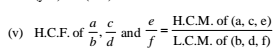
28.  LCM (Least Common Multiple)

There are two methods to find the LCM–

(a)    Factor method          (b)  Division method

1. For two numbers a and b if a < b, then L.C.M. of a and b is more than or equal to b.

2. If ratio between two numbers is a : b and their H.C.F. is x, then their L.C.M. = abx.