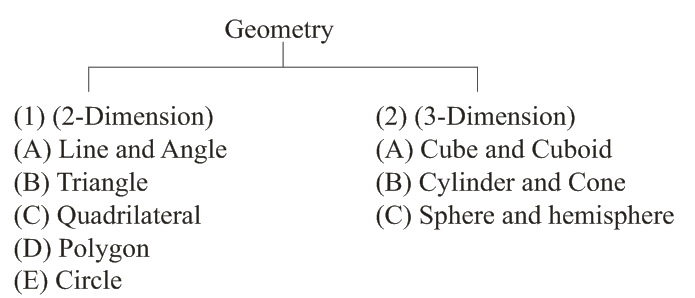
ज्यामिति (Geometry) फार्मूला और ट्रिक
L.A. (Line and Angle)
→ A line has no end points on either side 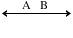
→ A line segment has two end points. 
→ A Ray has one end point 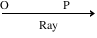
► Types of Angle:-
(i) Acute angle : – 0° < θ < 90°
(ii) Right Angle :– θ = 90°
(iii) Obtuse Angle : - 90° < θ < 180°
(iv) Straight Angle : - θ = 180°
(v) Reflex Angle : - 180° < θ < 360°
(vi) Complete Angle : - θ = 360°
► Relation between Angles:-
(i) Complementary Angle:-
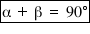
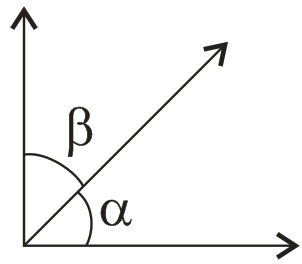
(ii) Supplementary Angle : -
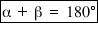
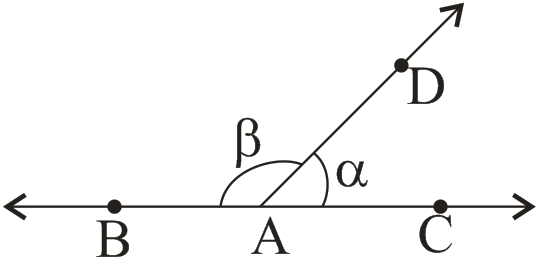
(iii) Adjacent Angle:-
→ The have a common vertex
→ They have a common arm
→ The non-common arms are on either side of the common arm.
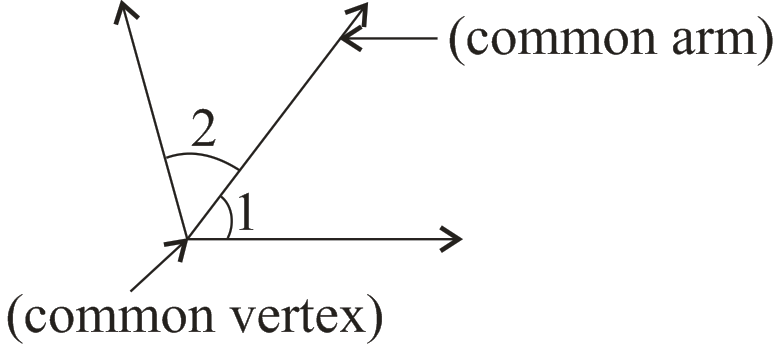
(iv) Linear pair Angles : - in last fig. If ∠1 + ∠2 = 180°
(v) Vertically opposite Angles : -
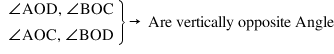
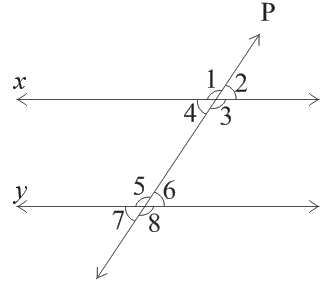
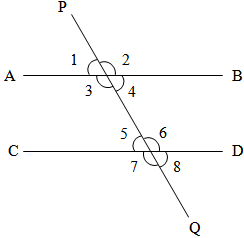
► Angle made by a transversal line :-
(i) Interior Angles : - ∠3, ∠4, ∠5, ∠6
(ii) External Angles : - ∠1, ∠2, ∠7, ∠8
(iii) Pair of corresponding Angles : -
∠1 and ∠5, ∠2 and ∠6, ∠4 and ∠7, ∠3 and ∠8
► 1. B → Triangle :-

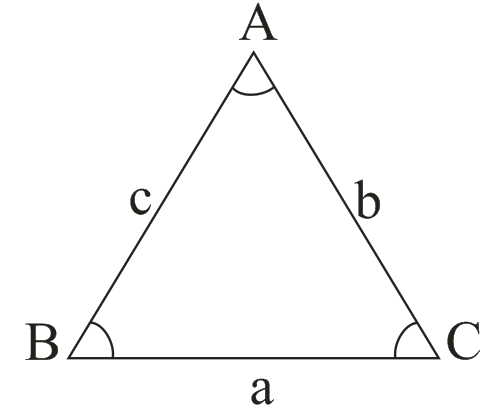
→ perimeter = (a + b + c)
sub perimeter=(a+b+c)/2
→ ∠A + ∠B + ∠C = 180°
→ a + b > c, c + a > b, c + b > a
→ 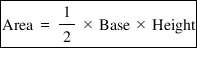
→ or. A = 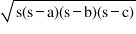
► Centres Triangle :-
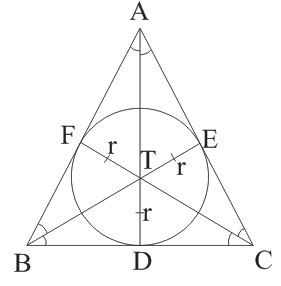
(i) In-centre : - The point of intersection of all the three angle bisectors.
→ 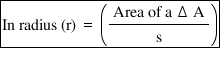
→ ∠BIC = 90 + 1/2 ∠A
(ii) circum - centre of triangle-
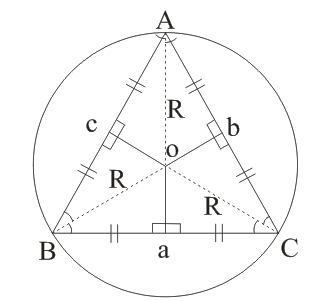
The points of intersection of perpendicular bisectors of three side.
→ ∠ BOC = 2.∠A
→ circumcentre in Right angle
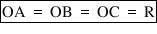
(iii) Centroid : - It is the point of intersection of all the three medians.
→ The centroid of triangle divides a median in ratio 2 : 1
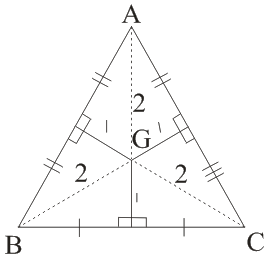
→ A median divides area of a ∆ in exactly two parts.
→ A centroid divides area of a ∆ in exactly three parts.
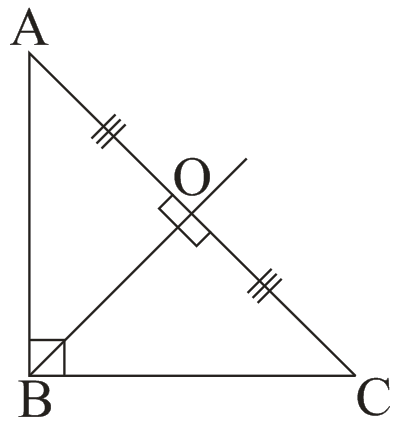
(iv) Ortho centre : - Point of intersection of all three altitude.
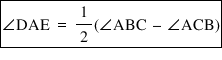
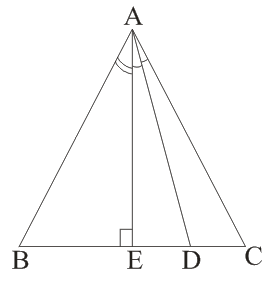
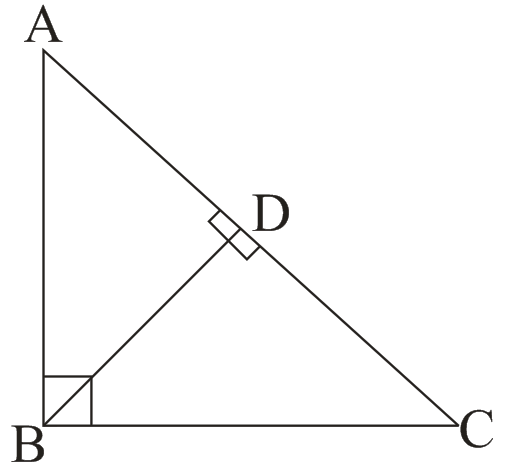
(iii) ∆ABC is a right -angle triangle and ∠B = 90°, then
(a) BD = 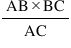
(b) AD = AB2/AC
(c) CD = 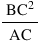
(d) 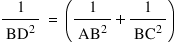
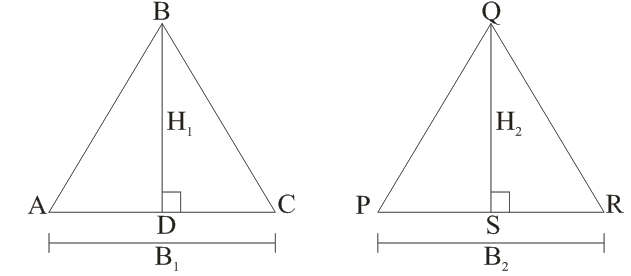
(iv) The ratio of the areas of two triangles is equal to the ratio of products of Base and its corresponding height
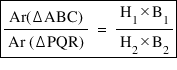
► I.C. Quadrilateral
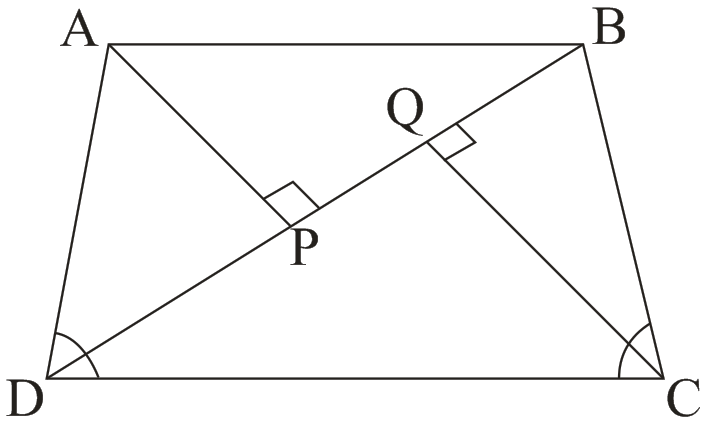
→ ∠A + ∠B + ∠C + ∠D = 360°
→ Area = 1/2 ×BD × (AP + CQ)
→ Pair of adjacent sides = (AB, BC), (BC, CD), (CD, DA), (DA, AB)
► Types of Quadrilateral
(i) Parallelogram (11gm):-
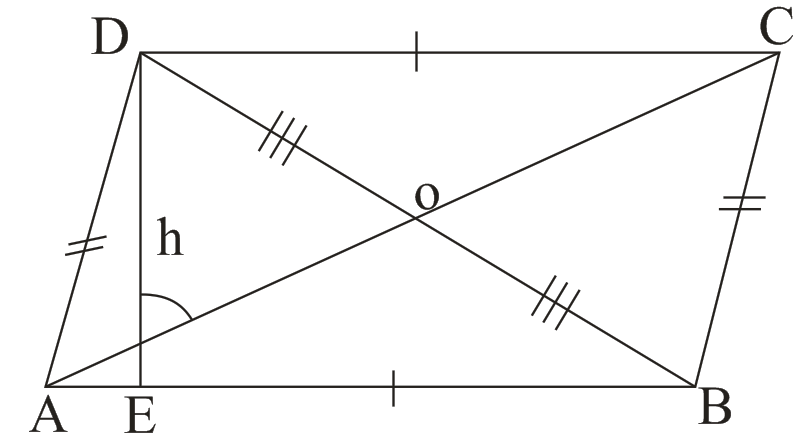
→ AB = CD, AD = BC
→ AB || CD, AD || BC
→ ∠A = ∠C, ∠B = ∠D
→ ∠A + ∠D = ∠A + ∠B = ∠B + ∠C = ∠C + ∠D = 180°
→ AO = OC, OB = OD
→ Bisectors of angles of a 11gm form a rectangle.
→AC2 + BD2 = (AB2 + BC2 + CD2 + AD2) = 2 (AB2 + BC2)
→ Area = (Base × Height) = AB × h = AB × AD sin θ
(ii) Rhombus:-
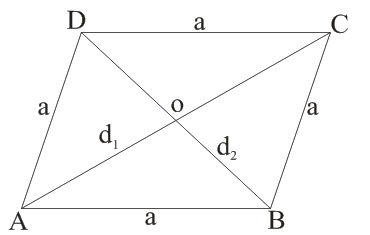
→ AB = BC = CD = AD
→ ∠A = ∠C, ∠B = ∠D
→ AO = OC, OB = OD
→ AO = OC, OB = OD
→ d12 + d22 = (AB2 + BC2 + CD2 + DA2) = 4a2
→ If d1 = d2, then ABCD is a square
→ Area = 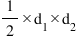
→ Perimeter = 4a
(iii) Trapezium:-

→ ∠A + ∠D = ∠B + ∠C = 180°
→ AB || CD
→ Median (EF) = 1/2 (AB + CD)
→ Area = 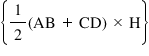
→ (AC2 + BD2) = (BC2 + AD2 + 2 × AB × CD)
→ (AC2 + BD2) = (BC2 + AD2 + 2 × AB × CD)
(iv) Rectangle :-
→ AB = CD, AD = BC
→ AB || CD, AD||BC
→ AC = BD = 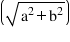
→ ∠A = ∠B = ∠C = ∠D = 90°
→ Area = (a × b)
→ Perimetre = 2 (a + b)
→ For the given perimenter of rectangle, a square has maximum area.
→ If 'p' is a point in rectangle, then (PA2 + PC2) = (PB2 + PD2)
(v) Square:-
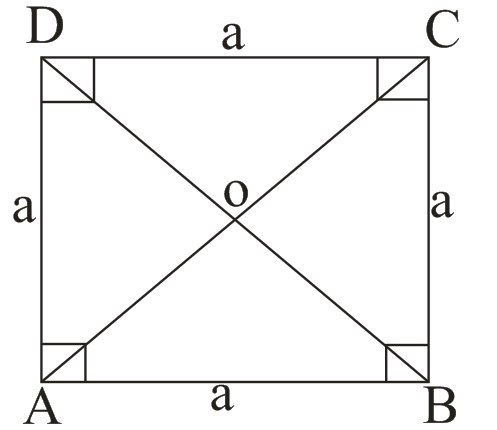
→ AB = BC = CD = AD = a
→ ∠A = ∠B = ∠C = ∠D = 90°
→ AB || BC, CD || AD
→ AC = BD, AC ⊥ BD
→ AC = BD = 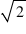 a
a
→ Area = a2 = (side)2
→ Perimetre = 4(a)
► I.D. Polygon
(For Regular Polygon)
→ Sum of interior angle = (n – 2) × 180°
→ Each exterior angle = 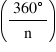
→ Sum of all exterior angle = 360°
→ Numbers of diagonals = 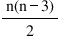
► I.E. circle
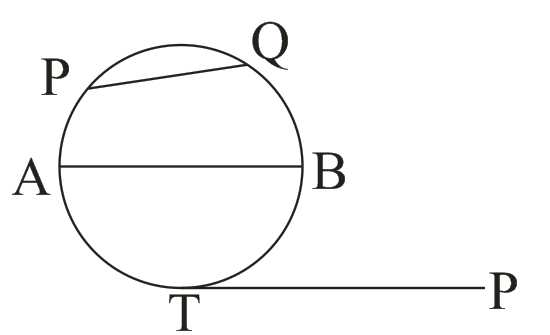
→ Perimeter = 2πr
→ Radius (r) = OA
→ Area = πr2
→ PQ → SECANT
→ Tangent → PT
→ Diameter = AB = 2r
► Properties of circle
(i) 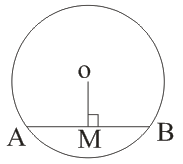
→ If OM ⊥ AB, then AM = MB
or
If AM = MB, then OM ⊥ AB
(ii)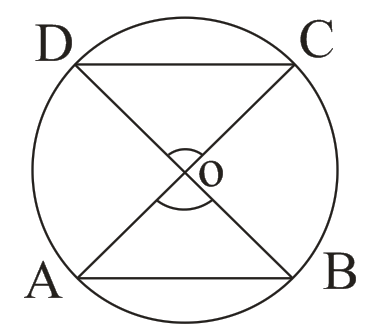
→ If AB = CD, then ∠AOB = ∠COD
or
If ∠AOB = ∠COD, then AB = CD
(iii)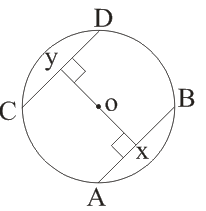
→ If OX = OY, then AB = CD
or
If AB = CD, then OX = OY
(iv)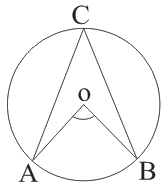
→ ∠AOB = ∠ACB
(v)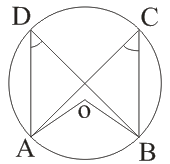
→ ∠ADB = ∠ACB
(vi)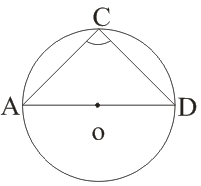
→ ∠ACD = 90° (The Angles in a semicircle is a Right angle)
(vii)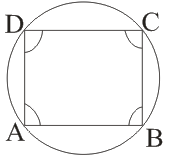
→ (∠A + ∠C = ∠B + ∠D = 180°)
(viii)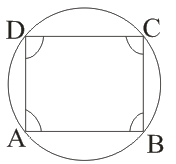
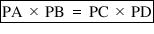
(ix)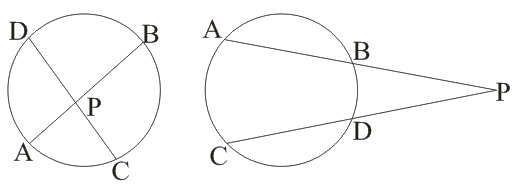
→ Length of tangent
Here XY = d
then PQ = RS = 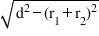
PS = RQ = 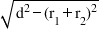
Concept 2
► 2.A → Cube and cuboid
→ Cube
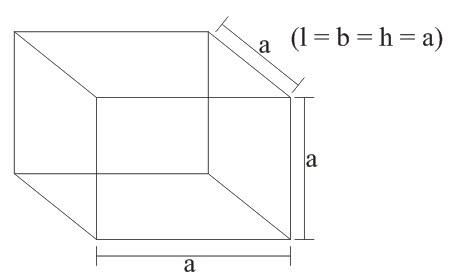
→ Volume = a3
→ Area = 6a2
→ Diagonal = 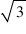 a
a
→ Cuboid
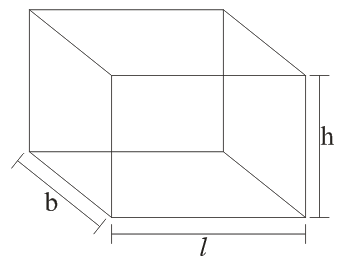
→ Volume = l × b × h cubic unit
→ Area of four walls = 2 (l + b) × h
→ Total surface area = 2 (lb + bh + hl)
→ Diagonal of cuboid = 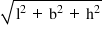
► 2.B. Cone and Cylinder
→ Right circular cylinder
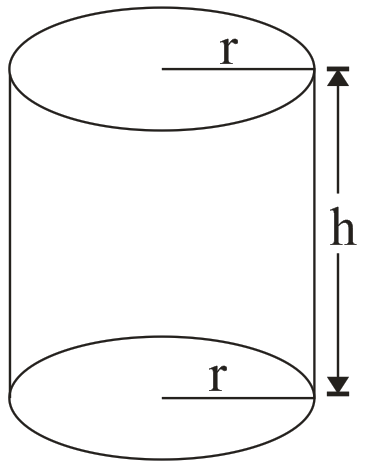
r → radius of base, h → height
→ V = Area of base × height
= π r2h cubic unit
→ Area of curved surface
= circumference of the base x height
= 2πrh sq. unit
→ Total surface Area = (curved surface Area) + (Area of two ends)
= 2πr (h + r)
→ Right circular cone
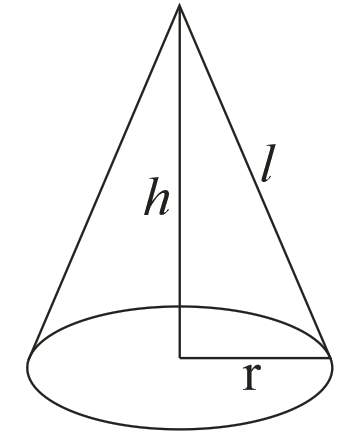
l = slant height = 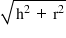
→ V = 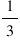 × area of base × height =
× area of base × height = 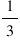 πr2h
πr2h
→ curved surface area = πrl sq. unit.
→ Total surface Area = (curved surface area + base area) = πr(l + r)
→ Volume of cone = 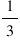 (volume of cylinder)
(volume of cylinder)
→ Volume of cylinder = 3 (Volume of cone)
{when r (cylinder) = r (cone) and h (cylinder) = h (cone)}
► 2.C. Sphere and Hemisphere
→ Sphere
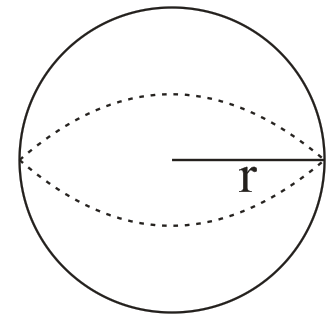
(i) V = 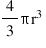 cubic units
cubic units
(ii) Surface area = 4πr2 sq. units
→ Spherical shell
If r = inner radius of spherical shell, and R = outer radius, then
(i) V = 4/3 π (R3 – r3)
(ii) Total surface area = 4π (R2 + r2)
→ Hemisphere
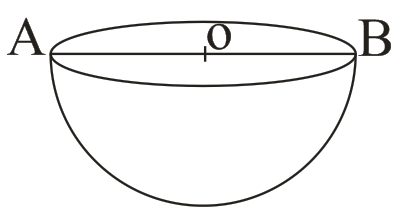
→ V = 2/3 πr3 cubic unit
→ curved surface area = 2πr2 sq. unit
→ Total surface area = 3πr2 sq. unit.
► 2.D. Frustum of a right circular cone
→ Frustum
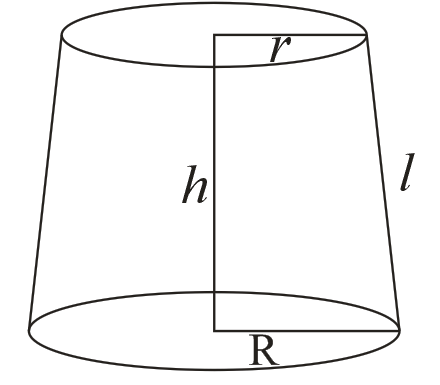
R → Radius of Base
r → Radius of top.
h → height of frustum
l → Slant height
(i) l = 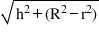 units
units
(ii) v = 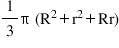 h cubic units
h cubic units
(iii) curved surface area = π (R + r) l + π (R2 + r2) sq. unit
= π [(R + r) l + (R2 + r2)] sq. unit
→ Right prism
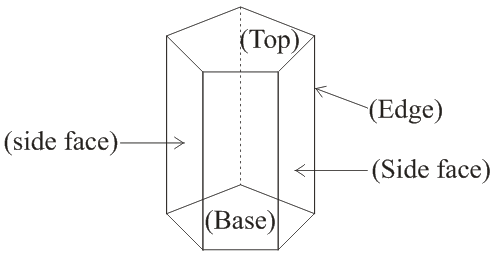
→ Number of vertices = 2n
→ Number of faces = (n + 2)
→ Volume of the prism = (Area of the base × height)
→ Lateral surface area of the prism = (perimeter of base × height)
→ Total surface Area = (Lateral surface area + 2 × Base Area)
Concept 3
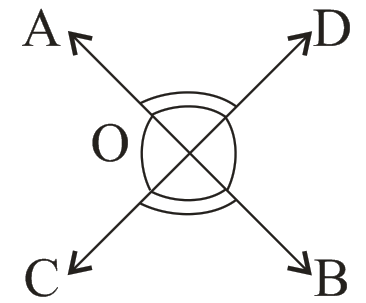
Theorem 1 → If two lines intersect each other, then vertical opposite angles are equal.
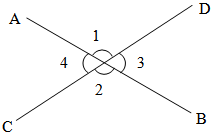
∠1 = ∠2 and ∠3 = ∠4
Parallel lines and transversal → A line intersects two or more lines at distinct points is called a transversal.
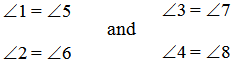
Theorem 2 → The sum of the angles of a triangle is 180°
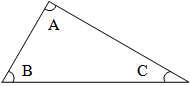
∠A + ∠B + ∠C = 180
Triangles : -
(i) Congruence of triangle → There are four rules.
a) SAS rule → Two triangles are congruent if two sides and included angle of one triangle are equal to sides and included angle of other triangle.
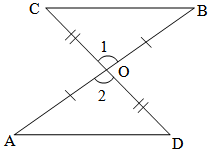
Now if OA = OB and OD = OC
then ∆AOD ≅ ∆BOC
b) ASA rule → Two triangle are congruent if two angles and included side of one are equal to two angles and included side of other triangle.
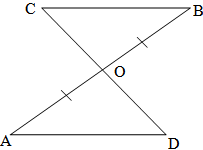
If OA = OD and ∠AOB = ∠COD, ∠ABO = ∠DCO
then ∆COD ≅ AOB
c) SSC rule → If three sides of one triangles are equal to three sides of another triangle then both triangle will be congruent.
d) RHS rule → If in two right angle triangles the hypotenuse and one side of a triangle are equal to hypotenuse and one side of another triangle, then two triangles are opposite to each other.
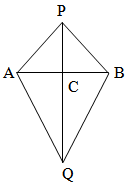
If AP = BP, AQ = BQ and PQ = PQ
∆PAQ ≅ ∆PBQ
Theorem 3 → If two sides of a triangle are unequal, then angle opposite to the longer side is larger.
Theorem 4 → The sum of any two sides of a triangle is always greater than the third side.
Similarity of triangle →
Theorem 5 → If a line is drawn parallel to one side of a triangle of a triangle to intersect the other two sides in distinct points, the other sides are divided in the same ratio.
The vice-versa is also true.
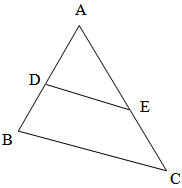
If DE || BC, then
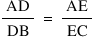 or
or 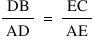 or
or 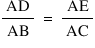
Theorem 6 → If in two triangles, sides of one triangle are proportional to the sides of another triangle then their corresponding angles are equal and hence the two triangles are similar.
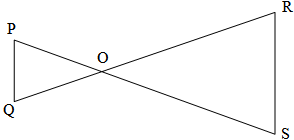
If PQ || RS, ∠P = ∠S and ∠Q = ∠R
then, ∆POQ ~ ∆SOR [Similar triangles]
Theorem 7 → The ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
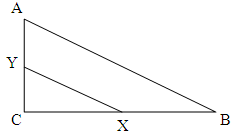
If XY || BA, ∠X = ∠Y and ∠A = ∠B
then ∆ABC ~ ∆XBY [Similar figures]
So, 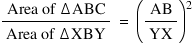
Theorem 8 →
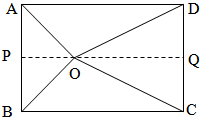
If 'O' is any point inside a rectangle then OB2 + OD2 = OA2 + OC2
Theorem 9 → Area of triangle by heron's formula
If a, b, c are 3 side of a triangle and semiperimeter S = 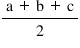
then area of triangle = 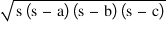
No comments:
Post a Comment